Časopis pro ty, kteří chtějí porozumět světu kolem sebe.
Časopis s obsahem recenzovaným odborníky.
Časopis s obsahem recenzovaným odborníky.
Příloha článku: KŘÍŽEK, M. (2025): Hostýn – reliéfem podmíněný symbol. Geografické rozhledy, 35(2), 14–15.
Odvození rovnice teoretické dohlednosti je velmi jednoduché a je postaveno na řešení Pythagorovy věty, kde L představuje teoretickou dohlednost, rz je poloměr referenční koule 6371 km a h je výška objektu nad referenční koulí, což v případě Hostýna představuje součet výšky nad mořem 735 a výšky rozhledny Františka Josefa I. na Hostýně, která je vysoká 15 m. V součtu tedy 750 m, což odpovídá 0,75 km.
L = ((rz + h)2 - rz 2) ½ = (rz2 +2rzh + h2 - rz 2) ½ = (2rzh + h2) ½. Tento vztah lze ještě zjednodušit, neboť, (2rzh + h2) ½ = (2rzh (1+ h/2rz)) ½ ≈ (2rzh) ½
Po dosazení platí, že: L = √(2·6371·0,75+0,752) = 97,76 km. Pro zjednodušenou verzi platí √(2·6371·0,75) = 97,757 km. Tedy teoretická dohlednost z rozhledny na Hostýně činí necelých 98 km. Jelikož díky atmosféře dochází k ohybu paprsků (tj. refrakci), což umožňuje dohlédnout za horizont a prodloužit skutečnou dohlednost průměrně o 6 až 7 %, v tomto případu 104 až 105 km. Samozřejmě ve skutečnosti dohlednost omezuje průhlednost atmosféry, která může být snížena vodními kapičkami mlhy, deštěm, sněhovými vločkami, prachem atd. Obecně nejlepší dohlednost následuje po přechodu studené fronty během podzimu či zimy.
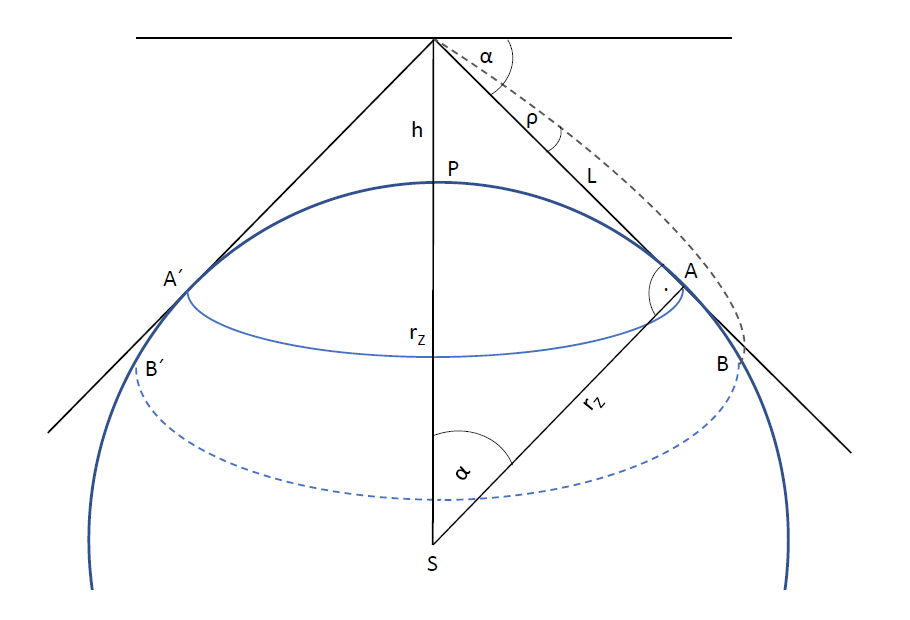
Obr. 1 Teoretická dohlednost. Poznámka: L = dohlednost; h = výška nad povrchem referenční koule; rz = poloměr referenční koule; α = úhel odpovídající výseči mezi tečným bodem a místem pozorovatele (resp. geodetická deprese obzoru); ρ = refrakční úhel; S = střed Země; P = poloha pozorovatele na referenční kouli; A, A´ = tečný bod (bod teoretické dohlednosti); B, B´ = bod skutečné dohlednosti.
Obr. 2 Matematický zápis rovnice teoretické dohlednosti na příkladu Hostýna.